Are you looking for an answer to the topic “What is the asymptote equation?“? We answer all your questions at the website Ecurrencythailand.com in category: +15 Marketing Blog Post Ideas And Topics For You. You will find the answer right below.
An asymptote of the curve y = f(x) or in the implicit form: f(x,y) = 0 is a straight line such that the distance between the curve and the straight line lends to zero when the points on the curve approach infinity. There are three types of asymptotes namely: Vertical Asymptotes.Example: Find the slant asymptote of y = (3x3 – 1) / (x2 + 2x). Let us divide 3x3 – 1 by x2 + 2x using the long division. Hence, y = 3x – 6 is the slant/oblique asymptote of the given function.

What is an asymptote equation example?
Example: Find the slant asymptote of y = (3x3 – 1) / (x2 + 2x). Let us divide 3x3 – 1 by x2 + 2x using the long division. Hence, y = 3x – 6 is the slant/oblique asymptote of the given function.
How do you find asymptotes in calculus?
A function f(x) will have the horizontal asymptote y=L if either limx→∞f(x)=L or limx→−∞f(x)=L. Therefore, to find horizontal asymptotes, we simply evaluate the limit of the function as it approaches infinity, and again as it approaches negative infinity.
Horizontal and Vertical Asymptotes – Slant / Oblique – Holes – Rational Function – Domain Range
Images related to the topicHorizontal and Vertical Asymptotes – Slant / Oblique – Holes – Rational Function – Domain Range

How do you write the equation of the asymptotes of hyperbolas?
Every hyperbola has two asymptotes. A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation y = k + (x – h) and the other with equation y = k – (x – h).
Finding the asymptotes
Images related to the topicFinding the asymptotes
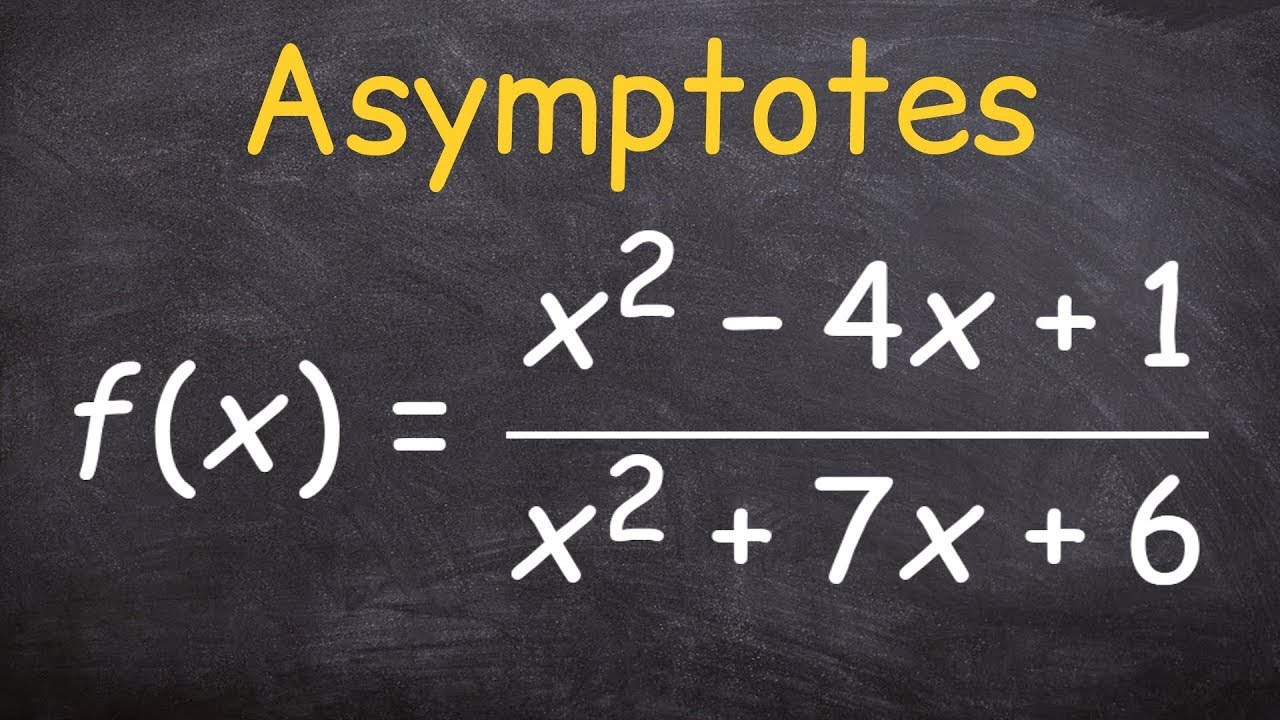
What are algebra asymptotes?
An asymptote is a line that a graph approaches without touching. If a graph has a horizontal asymptote of y = k, then part of the graph approaches the line y = k without touching it–y is almost equal to k, but y is never exactly equal to k.
How do you find the horizontal asymptote of a graph?
Given the Rational Function, f(x)= x/(x-2), to find the Horizontal Asymptote, we Divide both the Numerator ( x ), and the Denominator (x-2), by the highest degreed term in the Rational Function, which in this case, is the Term ‘x’. So, f(x)= (x/x)/[(x-2)/x].
Find the vertical and horizontal asymptotes
Images related to the topicFind the vertical and horizontal asymptotes
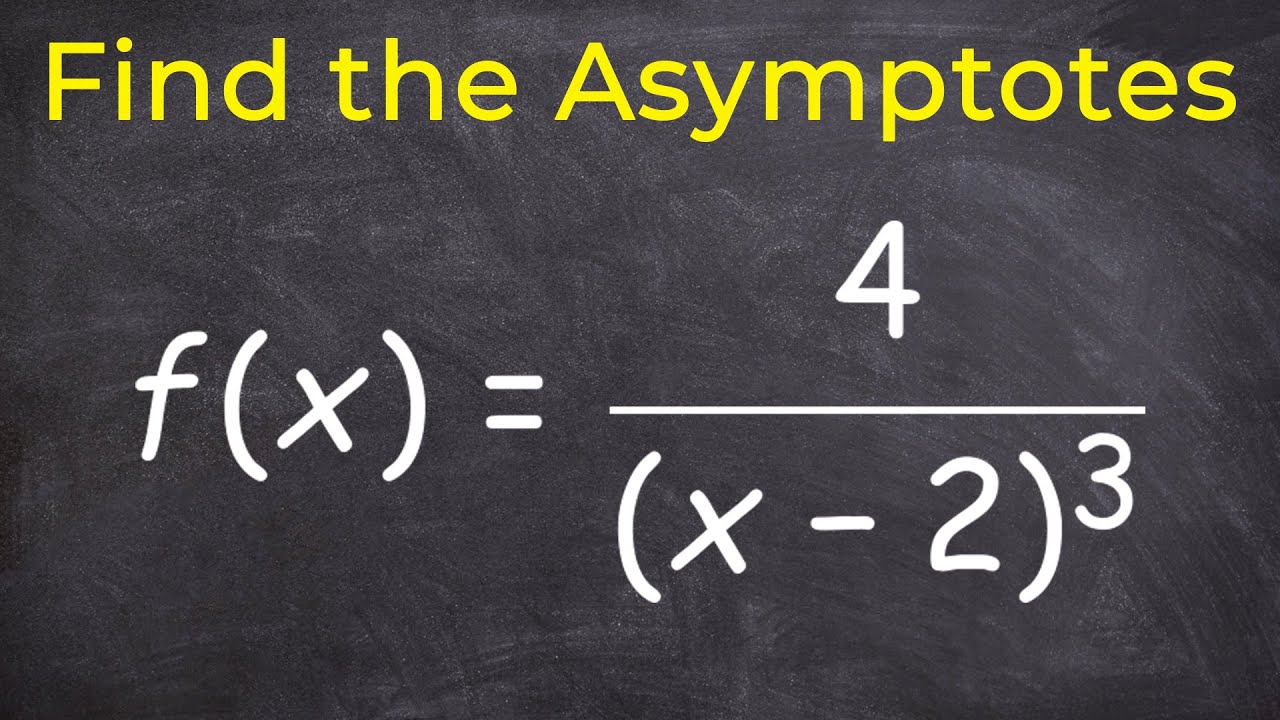
See some more details on the topic What is the asymptote equation? here:
How to Find the Equation of Asymptotes – dummies
Advance your pre-calculus knowledge and learn how to find the equation and slope of a hyperbola’s asymptotes with this handy guide.
Math Scene – Lesson 3 – Rational functions and Asymptotes
Vertical asymptotes can be found by solving the equation n(x) = 0 where n(x) is the denominator of the function ( note: this only applies if the numerator t(x) …
Asymptotes – Math24.net
An asymptote of a curve y = f (x) that has an infinite branch is called a line such that the distance between the point (x, f (x)) lying on the curve and …
Asymptote – Math is Fun
An asymptote is a line that a curve approaches, as it heads towards infinity.
What is a vertical asymptote?
A vertical asymptote is a vertical line that guides the graph of the function but is not part of it. It can never be crossed by the graph because it occurs at the x-value that is not in the domain of the function. A function may have more than one vertical asymptote.
How do you find the asymptote of a graph?
Vertical asymptotes can be found by solving the equation n(x) = 0 where n(x) is the denominator of the function ( note: this only applies if the numerator t(x) is not zero for the same x value). Find the asymptotes for the function . The graph has a vertical asymptote with the equation x = 1.
Related searches to What is the asymptote equation?
- horizontal asymptotes
- vertical asymptote equation
- what is the equation of the oblique asymptote h(x)=x^2-3x-4/x+2
- what is the asymptote equation
- horizontal asymptote equation
- asymptotes questions and answers pdf
- what is the equation of the horizontal asymptote
- what is the equation of the vertical asymptote
- what is the equation of the vertical asymptote and of the horizontal asymptote
- equation of asymptote of hyperbola
- vertical asymptote examples
- what is the equation of the oblique asymptote h(x)=x^2-x-2/x+1
- what is the equation of the vertical asymptote for the graph below
- equation of the asymptote calculator
- what is the equation of the asymptote for this function
- what is the equation of the vertical asymptote and of the horizontal asymptote brainly
- what is the equation of the asymptote of the hyperbola x^2/9-y^2/4=1
- asymptote meaning
Information related to the topic What is the asymptote equation?
Here are the search results of the thread What is the asymptote equation? from Bing. You can read more if you want.
You have just come across an article on the topic What is the asymptote equation?. If you found this article useful, please share it. Thank you very much.