Are you looking for an answer to the topic “When 3 altitudes of a triangle meet at a point they form?“? We answer all your questions at the website Ecurrencythailand.com in category: +15 Marketing Blog Post Ideas And Topics For You. You will find the answer right below.
In geometry, the three altitudes of a triangle meet at a common point, and that point is known as the
of the triangle.The point where all the three altitudes of a triangle intersect is called the orthocenter. Both the altitude and the orthocenter can lie inside or outside the triangle. In an equilateral triangle, the altitude is the same as the median of the triangle.The three angle bisectors of a triangle intersect at a single point. The point of concurrency of the angle bisectors is called the incenter. The three altitudes of a triangle are concurrent. The point of concurrency is called the orthocenter.

What are the 3 altitudes of a triangle intersect?
The point where all the three altitudes of a triangle intersect is called the orthocenter. Both the altitude and the orthocenter can lie inside or outside the triangle. In an equilateral triangle, the altitude is the same as the median of the triangle.
What is the name for the point where three altitude lines meet?
The three angle bisectors of a triangle intersect at a single point. The point of concurrency of the angle bisectors is called the incenter. The three altitudes of a triangle are concurrent. The point of concurrency is called the orthocenter.
What are Altitudes in a Triangle? (In depth explanation) | Don’t Memorise
Images related to the topicWhat are Altitudes in a Triangle? (In depth explanation) | Don’t Memorise

What are the 3 medians of a triangle intersect?
The point at which all the three medians of triangle intersect is called the orthocentre.
Where do altitudes intersect?
It turns out that all three altitudes always intersect at the same point – the so-called orthocenter of the triangle.
What is Incentre and Orthocentre?
incenter I, the point of which is equidistant from the sides of the triangle; orthocenter H, the point at which all the altitudes of the triangle intersect; centroid G, the point of intersection of the medians of the triangle.
What is the meaning of orthocenter?
Definition of orthocenter
: the common intersection of the three altitudes of a triangle or their extensions or of the several altitudes of a polyhedron provided these latter exist and meet in a point.
What special triangle whose intersection of its three altitudes is exactly on one of its vertices what vertex would it be?
This time we will look at a right triangle. It appears that the three altitudes are now intersecting in a single point at one of the vertices. Definition of concurrent: A number of lines are concurrent if they have exactly one point in common.
See some more details on the topic When 3 altitudes of a triangle meet at a point they form? here:
The point where the three altitudes of a triangle meet is called …
Orthocenter is a point which is formed by the intersection of the three altitudes of the triangle and these three altitudes are always concurrent.
Altitude (triangle) – Wikipedia
The three altitudes of a triangle intersect at the orthocenter, which for an acute triangle is inside the triangle. Altitudes can be used in the computation of …
Orthocenter of a triangle – math word definition
It turns out that all three altitudes always intersect at the same point – the so-called orthocenter of the triangle. The orthocenter is not always inside the …
Where does the altitude of a triangle intersect at? – AnswersToAll
When 3 altitudes of a triangle meet at a point they form a? The point where three altitudes of …
Where is the orthocenter of obtuse triangle?
The orthocenter is the intersection point of the altitudes drawn from the vertices of the triangle to the opposite sides. For an acute triangle, it lies inside the triangle. For an obtuse triangle, it lies outside of the triangle. For a right-angled triangle, it lies on the vertex of the right angle.
How many altitudes does an obtuse triangle have?
Every triangle has three altitudes. For an obtuse triangle, at least one of the altitudes will be outside of the triangle, as shown in the picture at the beginning of this section.
Proof: Triangle altitudes are concurrent (orthocenter) | Geometry | Khan Academy
Images related to the topicProof: Triangle altitudes are concurrent (orthocenter) | Geometry | Khan Academy

What is a altitude in a triangle?
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex). This line containing the opposite side is called the extended base of the altitude.
Do altitudes of a triangle always intersect?
It turns out that all three altitudes always intersect at the same point – the so-called orthocenter of the triangle. The orthocenter is not always inside the triangle. If the triangle is obtuse, it will be outside. To make this happen the altitude lines have to be extended so they cross.
How many altitudes are there in a triangle?
Answer: Three
A triangle has three altitudes– one end is at the vertex and the other on the opposite side. An altitude is also known as the height of the triangle.
What is the point where the three angle bisectors of a triangle intersect?
The three angle bisectors of the angles of a triangle meet in a single point, called the incenter .
What is altitude of a triangle class 7?
The altitude is the perpendicular drawn from the vertex to its opposite side and make a right angle with the base. The altitude may lie inside or outside the triangle.
Do altitudes bisect angles?
The isosceles triangle altitude bisects the angle of the vertex and bisects the base. It should be noted that an isosceles triangle is a triangle with two congruent sides and so, the altitude bisects the base and vertex.
What is centroid orthocenter and circumcenter?
For a triangle , let be the centroid (the point of intersection of the medians of a triangle), the circumcenter (the center of the circumscribed circle of ), and the orthocenter (the point of intersection of its altitudes). Then , , and are collinear and . Note that and can be located outside of the triangle.
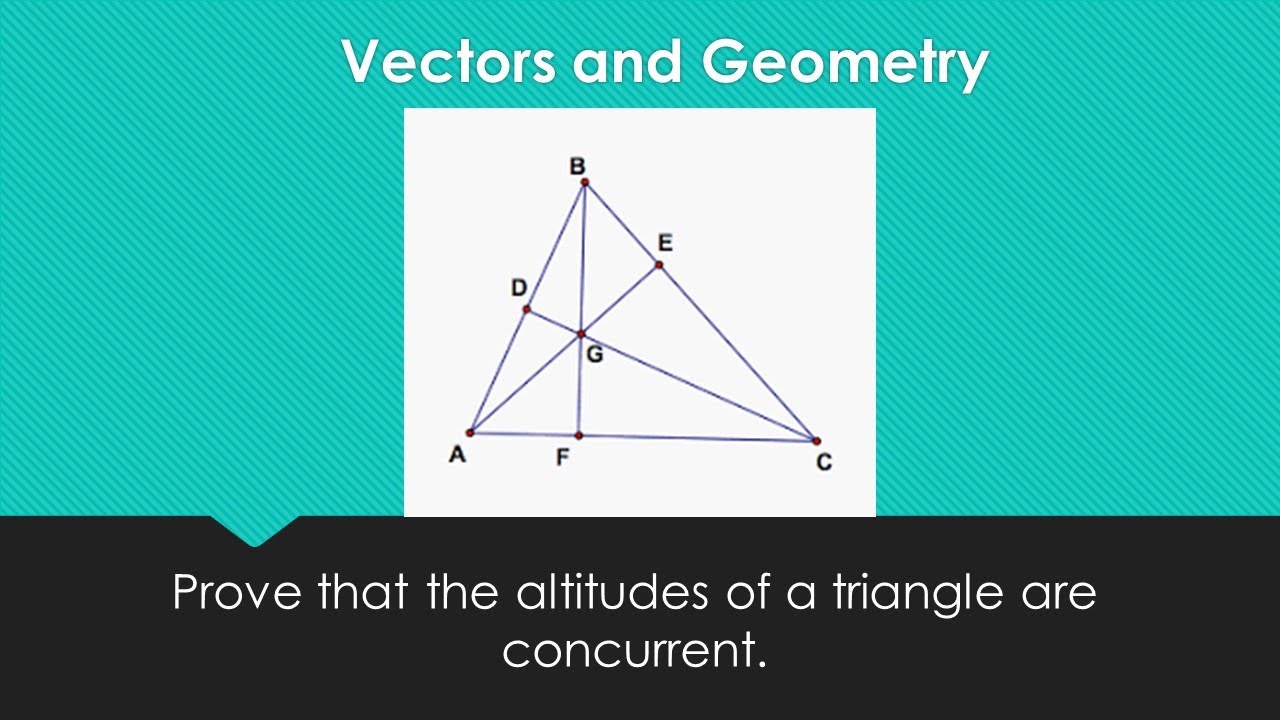
Vector proof that the altitudes of a triangles are concurrent
Images related to the topicVector proof that the altitudes of a triangles are concurrent
How incentre is formed?
Just like a centroid, an incenter is always inside the triangle and it is made by taking the intersection of the angle bisectors of all three vertices of the triangle.
What is centroid of a circle?
The point that may be considered as the center of a one– or two–dimensional figure i.e. the sum of the displacements of all points in the figure from such a point being zero. The centroid of a circle lies at the center of a circle that is also called as the radius of the circle from edges of a circle.
Related searches to When 3 altitudes of a triangle meet at a point they form?
- altitude of a triangle formula
- orthocenter of a triangle
- orthocenter
- the 3 medians of a triangle intersect at the
- the three altitudes of a triangle intersect at the
- altitude of a triangle
- altitude of a right triangle
- when 3 altitudes of a triangle meet at a point they form a triangle
- when 3 altitudes of a triangle meet at a point they form an ion
- when 3 altitudes of a triangle meet at a point they form an
- when 3 altitudes of a triangle meet at a point they form a right triangle
- the point at which the three angle bisectors of a triangle intersect
- when 3 altitudes of a triangle meet at a point they form a line
Information related to the topic When 3 altitudes of a triangle meet at a point they form?
Here are the search results of the thread When 3 altitudes of a triangle meet at a point they form? from Bing. You can read more if you want.
You have just come across an article on the topic When 3 altitudes of a triangle meet at a point they form?. If you found this article useful, please share it. Thank you very much.