Are you looking for an answer to the topic “Which matrix is decomposed in PCA?“? We answer all your questions at the website Ecurrencythailand.com in category: +15 Marketing Blog Post Ideas And Topics For You. You will find the answer right below.
Principal component analysis (PCA) is usually explained via an eigen-decomposition of the covariance matrix.How PCA uses this concept of eigendecomposition? Say, we have a dataset with ‘n’ predictor variables. We center the predictors to their respective means and then get an n x n covariance matrix. This covariance matrix is then decomposed into eigenvalues and eigenvectors.So, covariance matrices are very useful: they provide an estimate of the variance in individual random variables and also measure whether variables are correlated. A concise summary of the covariance can be found on Wikipedia by looking up ‘covariance’.

How is Eigen decomposition involved in PCA?
How PCA uses this concept of eigendecomposition? Say, we have a dataset with ‘n’ predictor variables. We center the predictors to their respective means and then get an n x n covariance matrix. This covariance matrix is then decomposed into eigenvalues and eigenvectors.
Why covariance matrix is used in PCA?
So, covariance matrices are very useful: they provide an estimate of the variance in individual random variables and also measure whether variables are correlated. A concise summary of the covariance can be found on Wikipedia by looking up ‘covariance’.
Visual Explanation of Principal Component Analysis, Covariance, SVD
Images related to the topicVisual Explanation of Principal Component Analysis, Covariance, SVD

What is decomposition PCA?
Principal component analysis (PCA). Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.
What is component matrix in PCA?
The elements of the Component Matrix are correlations of the item with each component. The sum of the squared eigenvalues is the proportion of variance under Total Variance Explained. The Component Matrix can be thought of as correlations and the Total Variance Explained table can be thought of as .
Why Eigen decomposition is used?
The most important application Eigen-value Eigen-vector decomposition is the decorrelation of your data or matrix. In turn, it can be used in the reduction of the dimensionality of your data.
Why is Eigen decomposition important?
Eigendecomposition is used to decompose a matrix into eigenvectors and eigenvalues which are eventually applied in methods used in machine learning, such as in the Principal Component Analysis method or PCA.
What is the significance of the covariance matrix and eigen vectors in PCA?
The eigenvectors and eigenvalues of a covariance (or correlation) matrix represent the “core” of a PCA: The eigenvectors (principal components) determine the directions of the new feature space, and the eigenvalues determine their magnitude.
See some more details on the topic Which matrix is decomposed in PCA? here:
Eigen Decomposition and PCA – Clairvoyant Blog
Of the many matrix decompositions, PCA uses eigendecomposition. ‘Eigen’ is a German word that means ‘own’. Here, a matrix (A) is decomposed …
Machine Learning — Singular Value Decomposition (SVD …
Machine Learning — Singular Value Decomposition (SVD) & Principal Component Analysis (PCA) · Misconceptions (optional for beginners) · Matrix diagonalization.
Principal component analysis – Wikipedia
Thus, the principal components are often computed by eigendecomposition of the data covariance matrix or singular value …
How Are Principal Component Analysis and Singular Value …
Singular Value Decomposition is a matrix factorization method utilized in many numerical applications of linear algebra such as PCA.
What is covariance matrix?
Covariance matrix is a type of matrix that is used to represent the covariance values between pairs of elements given in a random vector. The covariance matrix can also be referred to as the variance covariance matrix. This is because the variance of each element is represented along the main diagonal of the matrix.
What is the use of covariance matrix?
The covariance matrix provides a useful tool for separating the structured relationships in a matrix of random variables. This can be used to decorrelate variables or applied as a transform to other variables. It is a key element used in the Principal Component Analysis data reduction method, or PCA for short.
How is SVD used in PCA?
SVD gives you the whole nine-yard of diagonalizing a matrix into special matrices that are easy to manipulate and to analyze. It lay down the foundation to untangle data into independent components. PCA skips less significant components.
What does PCA return?
pca returns only the first d elements of latent and the corresponding columns of coeff and score . This option can be significantly faster when the number of variables p is much larger than d. pca returns all elements of latent . The columns of coeff and score corresponding to zero elements in latent are zeros.
StatQuest: PCA main ideas in only 5 minutes!!!
Images related to the topicStatQuest: PCA main ideas in only 5 minutes!!!
What is scree plot in PCA?
The scree plot is used to determine the number of factors to retain in an exploratory factor analysis (FA) or principal components to keep in a principal component analysis (PCA). The procedure of finding statistically significant factors or components using a scree plot is also known as a scree test.
What is a component matrix?
The component matrix shows the Pearson correlations between the items and the components. For some dumb reason, these correlations are called factor loadings. Ideally, we want each input variable to measure precisely one factor.
What is component transformation matrix?
The original factor or component loadings are transformed to the rotated loadings by postmultiplying the matrix of original loadings by the transformation matrix. The values in the transformation matrix are functions of the angle(s) of rotation of the factors or components.
What is pattern matrix?
The pattern matrix holds the loadings. Each row of the pattern matrix is essentially a regression equation where the standardized observed variable is expressed as a function of the factors. The loadings are the regression coefficients. The structure matrix holds the correlations between the variables and the factors.
Why is matrix decomposition important?
Many complex matrix operations cannot be solved efficiently or with stability using the limited precision of computers. Matrix decompositions are methods that reduce a matrix into constituent parts that make it easier to calculate more complex matrix operations.
What is spectral decomposition of a matrix?
When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called “spectral decomposition”, derived from the spectral theorem.
Does every matrix have an eigendecomposition?
Every square matrix of degree n does have n eigenvalues and corresponding n eigenvectors. These eigenvalues are not necessary to be distinct nor non-zero. An eigenvalue represents the amount of expansion in the corresponding dimension.
When can a matrix be diagonalized?
A square matrix is said to be diagonalizable if it is similar to a diagonal matrix. That is, A is diagonalizable if there is an invertible matrix P and a diagonal matrix D such that. A=PDP^{-1}.
What is eigenvectors of the covariance matrix?
In other words, the largest eigenvector of the covariance matrix always points into the direction of the largest variance of the data, and the magnitude of this vector equals the corresponding eigenvalue.
Eigendecomposition and PCA
Images related to the topicEigendecomposition and PCA
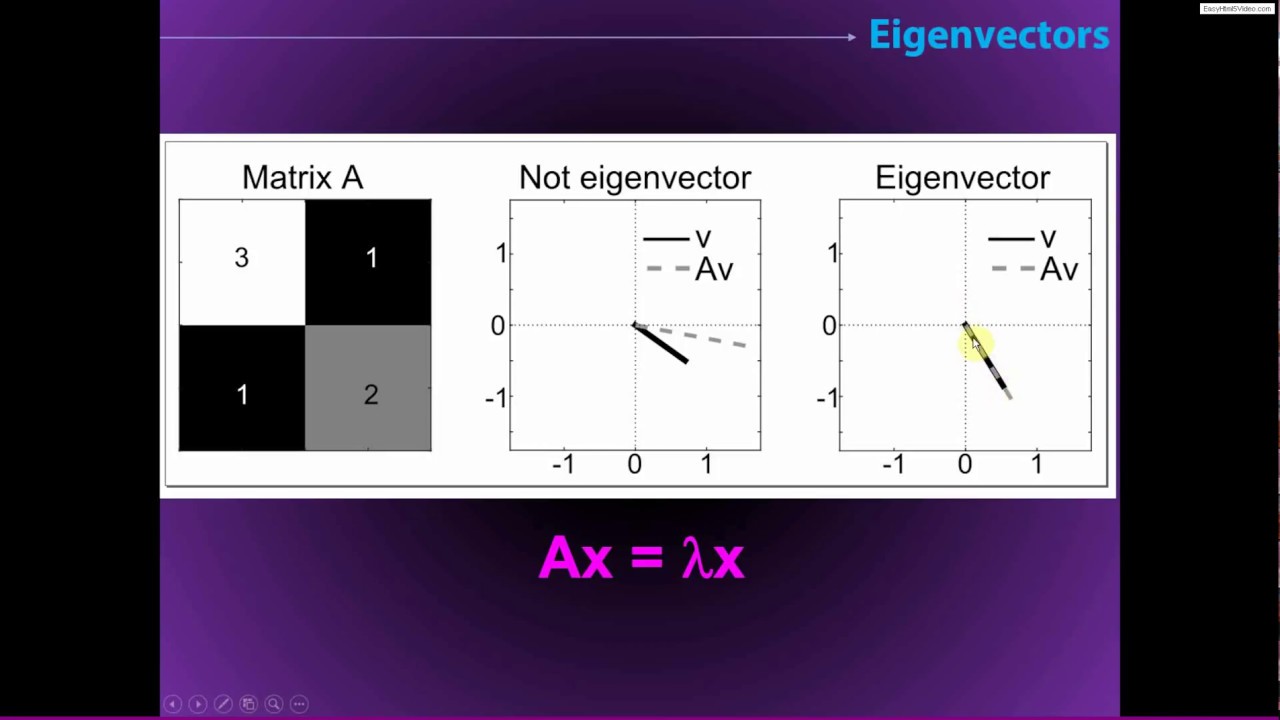
What do eigenvalues tell you about a matrix?
An eigenvalue is a number, telling you how much variance there is in the data in that direction, in the example above the eigenvalue is a number telling us how spread out the data is on the line. The eigenvector with the highest eigenvalue is therefore the principal component.
What do eigenvalues and eigenvectors represent?
The Eigenvector is the direction of that line, while the eigenvalue is a number that tells us how the data set is spread out on the line which is an Eigenvector.
Related searches to Which matrix is decomposed in PCA?
- covariance matrix in pca
- Implement PCA with svd
- Eigenvector and PCA
- pca
- which matrix is decomposed in pca python
- which matrix is decomposed in pca for
- implement pca with svd
- eigenvector and pca
- which matrix is decomposed in pca model
- singular value decomposition in matrix
- PCA example
- pca calculator
- PCA
- Singular value decomposition
- Covariance matrix in PCA
- singular value decomposition
- pca example
Information related to the topic Which matrix is decomposed in PCA?
Here are the search results of the thread Which matrix is decomposed in PCA? from Bing. You can read more if you want.
You have just come across an article on the topic Which matrix is decomposed in PCA?. If you found this article useful, please share it. Thank you very much.